Фракталы. Что это такое?
Фракталы известны науке уже больше века. Они хорошо изучены и широко используются не только учёными в своих расчётах, но и во многих других областях нашей жизни. И при всём этом, сформулировать их определение пока не удаётся.
Хотя можно выделить основные признаки фракталов. Самоподобие и маштабирование.
Давайте рассмотрим небольшой пример. Мы каждый день видим деревья, будь то на какой-нибудь фотографии или по пути на работу, но не всегда замечаем как устроено само дерево. От ствола отходят ветки, от веток отростки поменьше. Так, сравнив ствол дерева и его ветки, окажется, что они подобны друг другу по строению. Это и есть самоподобие.
Но ведь деревья не являются фракталами! Фракталы обладають бесконечным числом итераций, то есть повторяют сами себя бесконечное количество раз. Это и отличает деревья и другие самоподобные объекты от фракталов.
Получается, если фракталы - бесконечные самоподобные фигуры, то их не существует в природе? Всё верно. Они не возможны в нашем мире, но широко применяются, к примеру, в играх. С их помощью в виртуальных мирах рисуются деревья, трава и многое другое. Так же они применяются в физике(моделирование сложных процессов и материалов), биологии(моделирование популяций, описание сложных ветвящихся структур), технике(фрактальные антенны), экономике. Существуют алгоритмы сжатия изображений с помощью фракталов. В общем, полезная штука эти фракталы.
Давайте теперь рассмотрим виды фракталов. Их всего три:
-
Геометрические – строятся на основе исходной фигуры (линии, многоугольника или многогранника) путем ее дробления и выполнения различных преобразований полученных фрагментов
-
Алгебраические – строятся на основе алгебраических формул
-
Стохастические – получаются, если в итерационном процессе случайным образом изменять какие-либо параметры
Геометрические фракталы.
Геометрические фракталы, как уже было сказано, строятся на основе исходной фигуры (линии, многоугольника или многогранника) путем ее дробления и выполнения различных преобразований полученных фрагментов.
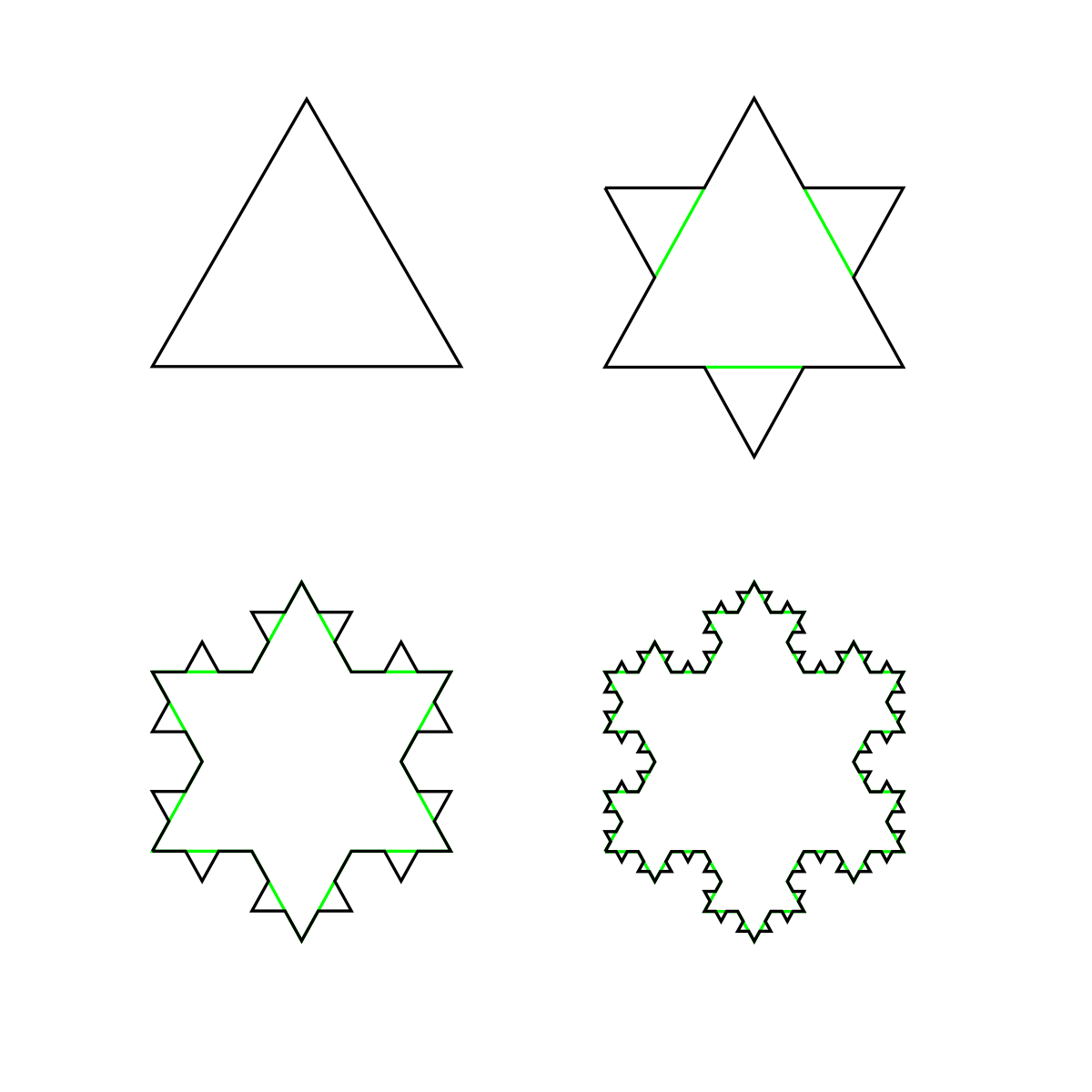
Так например, устроена снежинка Коха. Изначально это был всего лишь треугольник, но затем каждую сторону поделили на три равных отрезка, и средний отрезок достраивается до правильного треугольника. Это первая итерация.
Дальше на каждом отрезке каждой стороны производится точно такая же операция. Это вторая итерация. Так продолжать можно до бесконечности.
Снежинка Коха - самый простой пример геометрических фракталов.
Алгeбрарические фракталы.
Свое название они получили за то, что их строят, на основе алгебраических формул иногда весьма простых. Методов получения алгебраических фракталов несколько. Один из методов представляет собой многократный (итерационный) расчет функции Zn+1=f(Zn), где Z - комплексное число, n - колличество итераций, а f некая функция. Расчет данной функции продолжается до выполнения определенного условия. И когда это условие выполнится - на экран выводится точка. При этом значения функции для разных точек комплексной плоскости может иметь разное поведение:
-
С течением времени стремится к бесконечности
-
Стремится к 0
-
Принимает несколько фиксированных значений и не выходит за их пределы
-
Поведение хаотично, без каких либо тенденций
Мандельброта

Множество Жулиа

Стохастические фракталы.

Фракталы, при построении которых в итеративной системе случайным образом изменяются какие-либо параметры, называются стохастическими. Термин «стохастичность» происходит от греческого слова, обозначающего «предположение».
Стохастические фракталы, смоделированные компьютерной программой, очень похожи на природные творения - несимметричные деревья, изрезанные береговые линии, горный массив и т.д.
Примером стохастического фрактала является плазма. Для ее построения берется прямоугольник и для каждого его угла определяется цвет. Далее находится центральная точка прямоугольника и раскрашивается в цвет равный среднему арифметическому цветов по углам прямоугольника плюс некоторое случайное число. Чем больше случайное число, тем более «рваным» будет рисунок. Если посмотреть на этот фрактал в разрезе, то мы увидим, что он объемный и имеет «шероховатость». Именно из-за этой «шероховатости» есть очень важное применение этого фрактала.
Допустим нужно описать форму горы. Обычные фигуры из Евклидовой геометрии тут не помогут, ведь они не учитывают рельеф поверхности. Но при совмещении обычной геометрии с фрактальной можно получить ту самую «шероховатость» горы.